在数学（线性代数）中，只要函数$f: A \rightarrow B$ 如果对于每个 $x$ 和 $y$ 在域中 $A$ 具有以下属性： $f(x) + f(y) = f(x+y)$. 根据定义，ReLU 是$max(0,x)$. 因此，如果我们将域从$(-\infty, 0]$ 或者 $[0, \infty)$那么函数是线性的。然而，很容易看出$f(-1) + f(1) \neq f(0)$. 因此，根据定义，ReLU 不是线性的。

然而，ReLU 如此接近线性，以至于这常常使人们感到困惑，并想知道如何将它用作通用逼近器。以我的经验，考虑它们的最佳方式就像黎曼和。您可以使用许多小矩形来逼近任何连续函数。ReLU 激活可以产生很多小矩形。事实上，在实践中，ReLU 可以制作相当复杂的形状并逼近许多复杂的域。

我也想澄清另一点。正如之前的答案所指出的，神经元在 Sigmoid 中不会死亡，而是消失了。这样做的原因是因为 sigmoid 函数的导数最大为 0.25。因此，经过这么多层之后，您最终会乘以这些梯度，并且小于 1 的非常小的数字的乘积往往会很快变为零。

因此，如果你正在构建一个具有很多层的深度学习网络，你的 sigmoid 函数将基本上很快停滞不前并且或多或少变得无用。

关键是消失来自梯度相乘而不是梯度本身。

我了解 ReLU 的优点，即在反向传播期间避免死神经元。

这并不完全正确。神经元没有死。如果您使用类似 sigmoid 的激活，在一些迭代之后，大多数神经元的梯度值会饱和。梯度的值会很小，学习的过程会很慢。这是在类似 sigmoid 的激活函数中消失和爆炸的梯度。相反，如果使用非线性，可能会发生死神经元ReLU，这称为死 ReLU。

如果输出是线性的，我无法理解为什么 ReLU 被用作激活函数

绝对不是线性的。作为一个简单的定义，线性函数是在其域中的输入具有相同导数的函数。

线性函数在经济学中很流行。它很有吸引力，因为它简单且易于数学处理。它有许多重要的应用。线性函数是那些图形是直线的函数。线性函数具有以下性质：

$f(ax + by) = af(x) + bf(y)$

ReLU不是线性的。简单的答案是ReLU的输出不是一条直线，它在 x 轴处弯曲。更有趣的一点是这种非线性的结果是什么。简单来说，线性函数允许您使用直线剖析特征平面。但是由于 s 的非线性ReLU，您可以在特征平面上构建任意形状的曲线。

ReLU可能有一个缺点，即它的期望值。的输出没有限制，Relu其期望值不为零。Tanh比它更受欢迎，sigmoid因为它的期望值等于 0，并且更深层次的学习发生得更快。虽然ReLU没有这个优势batch normalization解决了这个问题。

您也可以参考此处和此处了解更多信息。

在 NN 中使用激活函数的主要原因是引入非线性。ReLU 在引入它方面做得很好。

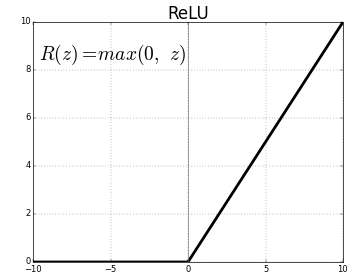
我选择 ReLU 作为激活函数的三个原因

• 首先它是非线性的（虽然它的行为类似于 x > 0 的线性函数）
• ReLU 的计算成本很低。由于它是简单的数学运算，模型运行时间更短
• ReLU 通过将最小值设置为 0 来诱导稀疏性