任何人都可以解释差异并举例说明如何使用这三种分析吗？
我到处搜索，但找不到具有真实值的真实示例，以了解如何使用这些分析和计算数据，只有很多公式，没有任何真实示例就难以理解。正如我试图理解的那样，很难区分哪些方程/公式属于 LDA，哪些属于 FDA。
例如，假设有这样的数据：
x1 x2 class
1 2 a
1 3 a
2 3 a
3 3 a
1 0 b
2 1 b
2 2 b
让我们说一些测试数据：
x1 x2
2 4
3 5
3 6
那么如何通过所有这三种方法使用这些数据呢？最好看看如何手动计算所有内容，而不是使用一些在幕后计算所有内容的数学包。
PS我只找到了这个教程： http: //people.revoledu.com/kardi/tutorial/LDA/LDA.html#LDA。它展示了如何使用 LDA。
“Fisher's Discriminant Analysis”只是2类情况下的LDA。当只有 2 个类别时，手动计算是可行的，并且分析与多重回归直接相关。LDA是Fisher关于任意类情况的思想的直接扩展，并使用矩阵代数设备（如特征分解）来计算它。因此，“Fisher 判别分析”这个术语在今天看来已经过时了。应改为使用“线性判别分析”。另请参阅。具有 2 个以上类别（多类别）的判别分析通过其算法是规范的（将判别式提取为规范变量）；罕见术语“典型判别分析”
在计算判别函数后，Fisher 使用当时称为“Fisher 分类函数”的方法对对象进行分类。如今，在 LDA 程序中使用更通用的贝叶斯方法对对象进行分类。
对于您对 LDA 的解释请求，我可能会将我的答案发送给您： LDA 中的提取、LDA中的分类、相关程序中的 LDA 。还有这个，这个，这个问题和答案。
就像 ANOVA 需要假设等方差一样，LDA 需要假设类的等方差-协方差矩阵（在输入变量之间）。这个假设对于分析的分类阶段很重要。如果矩阵显着不同，则观察值将倾向于分配给变异性较大的类别。为了克服这个问题，发明了QDA。QDA 是对 LDA 的修改，它允许类协方差矩阵的上述异质性。
如果您具有异质性（例如通过 Box 的 M 检验检测到）并且您手头没有 QDA，您仍然可以在使用分类时判别式的单个协方差矩阵（而不是合并矩阵）的制度中使用 LDA . 这部分地解决了这个问题，尽管不如 QDA 有效，因为 - 正如刚才指出的那样 - 这些是判别式之间的矩阵，而不是原始变量之间的矩阵（哪些矩阵不同）。
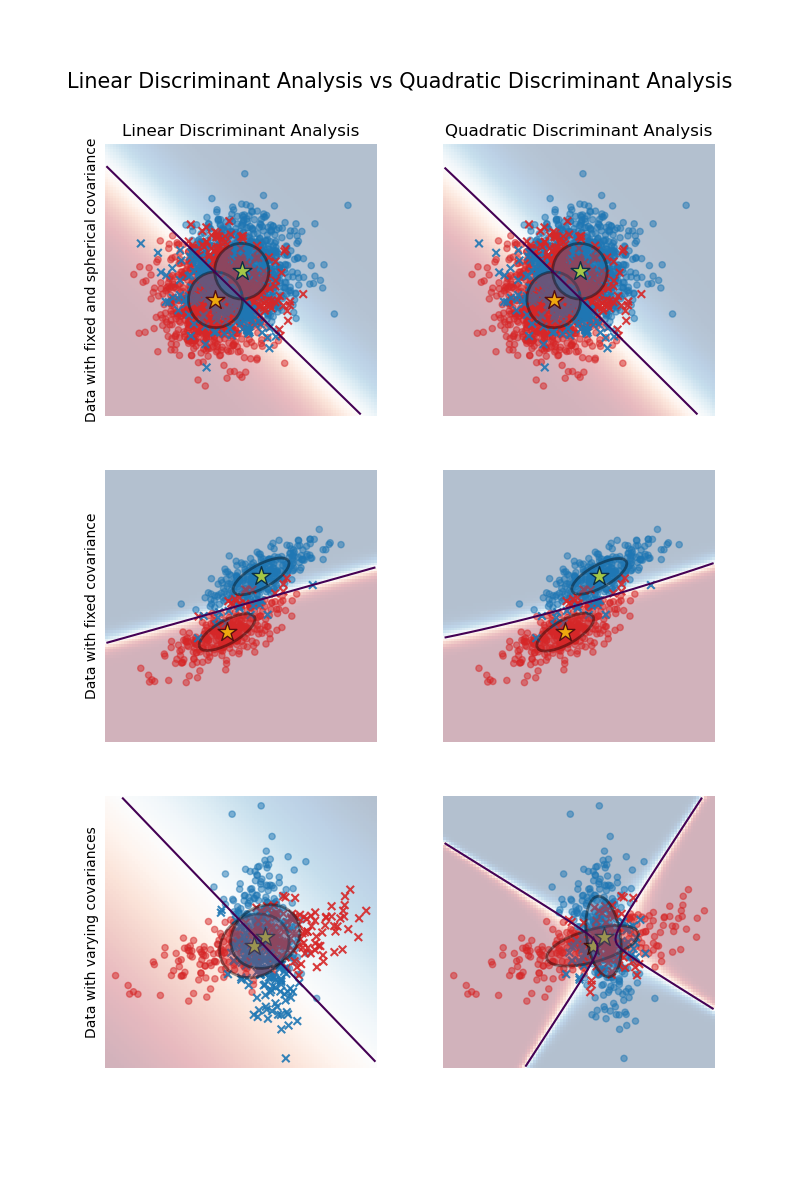
让我自己分析您的示例数据。
回复@zyxue 的回答和评论
LDA 是您在答案中定义的 FDA。LDA首先提取线性构造（称为判别式），以最大化间隔到内部的分离，然后使用它们执行（高斯）分类。如果（如您所说）LDA 与提取判别式的任务无关 LDA 似乎只是一个高斯分类器，则根本不需要名称“LDA”。
这是LDA 假设类的正态性和方差-协方差同质性的分类阶段。LDA的提取或“降维”阶段假设线性和方差-协方差同质性，这两个假设共同使“线性可分性”成为可能。（我们使用单个池矩阵来生成判别式，因此该判别式在类内协方差矩阵中具有恒等池化，这使我们有权将同一组判别式应用于所有类。如果所有都相同，则所述内-类协方差都是相同的，同一性；使用它们的权利成为绝对的。）
高斯分类器（LDA 的第二阶段）使用贝叶斯规则通过判别器将观察值分配给类。通过直接利用原始特征的所谓Fisher线性分类函数可以实现相同的结果。然而，贝叶斯基于判别式的方法有点通用，因为除了使用一种默认方式（池化矩阵）之外，它还允许使用单独的类判别协方差矩阵。此外，它将允许基于判别式子集进行分类。
当只有两个类时，LDA 的两个阶段可以一起描述一次，因为“潜在提取”和“观察分类”减少到相同的任务。
正如@ttnphns 所建议的那样，我发现很难同意 FDA 是两个类别的 LDA。
我推荐 Ali Ghodsi 教授关于这个主题的两场内容丰富且精彩的讲座：
对我来说，LDA 和 QDA 是相似的，因为它们都是具有高斯假设的分类技术。两者之间的一个主要区别是 LDA 假设两个类的特征协方差矩阵相同，这导致了线性决策边界。相比之下，QDA 不那么严格，并且允许针对不同类别使用不同的特征协方差矩阵，这导致了二次决策边界。请参阅scikit-learn中的下图，了解二次决策边界的外观。
对子图的一些评论：
另一方面，FDA 是一个非常不同的物种，与高斯假设无关。FDA 试图做的是找到一个线性变换来最大化类间平均距离，同时最小化类内方差。第二讲很好地解释了这个想法。与LDA/QDA相比，FDA不做分类，虽然FDA发现转换后得到的特征可以用于分类，例如使用LDA/QDA，或SVM等。