据我了解,英国学校教导标准偏差是使用以下方法找到的:
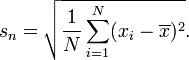
而美国学校教授:
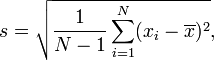
(无论如何在基本水平上)。
这引起了我的一些学生的问题,他们过去在网上搜索过,但发现错误的解释。
为什么有区别?
使用简单的数据集说 10 个值,如果应用错误的方法(例如在考试中)会有多大程度的错误?
据我了解,英国学校教导标准偏差是使用以下方法找到的:
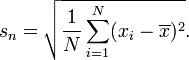
而美国学校教授:
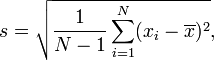
(无论如何在基本水平上)。
这引起了我的一些学生的问题,他们过去在网上搜索过,但发现错误的解释。
为什么有区别?
使用简单的数据集说 10 个值,如果应用错误的方法(例如在考试中)会有多大程度的错误?
第一个公式是总体标准差,第二个公式是样本标准差。第二个公式也与方差的无偏估计量有关-有关更多详细信息,请参见维基百科。
我想(这里)在英国,他们没有区分高中的样本和人口。他们当然不会触及诸如有偏估计量之类的概念。
因为还没有人回答最后一个问题——即量化两个公式之间的差异——让我们来解决这个问题。
出于许多原因,比较标准偏差是根据它们的比率而不是它们的差异来比较合适的。比率是
近似值可以看作是截断平方根的(交替)泰勒级数,表明误差不能超过=. 这确定了一次近似值(对于我们的目的)绰绰有余是或更大。
立即发现两个 SD 估计值彼此相差(大约)10% 以内超过, 5% 以内一次超过, 等等。显然,对于许多目的,这些差异是如此之小,以至于使用哪个公式都无关紧要,尤其是当 SD 旨在描述数据的传播或进行半定量评估或预测时(例如在使用 68-95 -99.7 经验法则)。比较时差异甚至不那么重要SD,例如在比较两个数据集的分布时。(当数据集数量相等时,差异实际上完全消失了,两个公式得出相同的结论。)可以说,这些是我们试图教初学者的推理形式,所以如果学生开始担心使用哪个公式,这可能被视为文本或课程未能强调真正重要的标志。
我们可能要注意非常小的情况. 在这里,人们可能正在使用测试而不是测试,例如。在这种情况下,必须使用表格或软件使用的标准偏差公式。(这不是一个公式是错还是对的问题;这只是一个一致性要求。)大多数表格使用, 不是:这是小学教学大纲中的一个地方,课本和老师需要明确使用哪个公式。
这是贝塞尔的修正。美国版显示的是样本标准差的公式,上面的英国版是样本的标准差。
我不确定这纯粹是美国与英国的问题。本页的其余部分摘自我写的一个常见问题解答(http://www.graphpad.com/faq/viewfaq.cfm?faq=1383)。
如何计算分母为 n-1 的 SD
计算每个值与样本均值之差的平方。
将这些值加起来。
将总和除以 n-1。结果称为方差。
取平方根以获得标准偏差。
为什么是n-1?
为什么在计算标准差时除以 n-1 而不是 n?在步骤 1 中,您计算每个值与这些值的平均值之间的差值。你不知道人口的真实平均值;您所知道的只是样本的平均值。除了样本均值恰好等于总体均值的极少数情况外,数据将更接近样本均值而不是真实总体均值。因此,您在步骤 2 中计算的值可能会比在步骤 1 中使用真实总体平均值时的值小一些(并且不能更大)。为了弥补这一点,除以 n-1 而不是比 nv 这称为贝塞尔校正。
但是为什么是n-1?如果您知道样本均值以及除一个值之外的所有值,您可以计算最后一个值必须是什么。统计学家说有 n-1 个自由度。
何时应使用 n 而不是 n-1 的分母计算 SD?
统计书籍通常显示两个计算 SD 的方程,一个使用 n,另一个使用 n-1,在分母中。有些计算器有两个按钮。
n-1 方程用于分析数据样本并希望得出更一般性结论的常见情况。以这种方式计算的 SD(以 n-1 为分母)是您对总体总体中 SD 值的最佳猜测。
如果您只是想量化一组特定数据的变化,并且不打算外推得出更广泛的结论,那么您可以使用 n 作为分母来计算 SD。得到的 SD 是那些特定值的 SD。如果您想估计从中抽取这些点的总体的 SD,那么以这种方式计算 SD 是没有意义的。仅当没有从总体中抽样时,在分母中使用 n 才有意义,并且不希望做出一般性结论。
科学的目标几乎总是概括,因此不应使用分母为 n 的方程。我能想到的唯一可能有意义的例子是量化考试成绩之间的差异。但更好的是显示每个分数的散点图,或频率分布直方图。