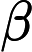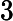我试图了解如何最好地模拟一个变量，随着时间的推移，我获得了越来越详细的预测变量。例如，考虑对违约贷款的回收率进行建模。假设我们有一个包含 20 年数据的数据集，而在前 15 年中，我们只知道贷款是否被抵押，但对抵押品的特征一无所知。然而，在过去五年中，我们可以将抵押品分为一系列类别，这些类别有望很好地预测回收率。
鉴于此设置，我想为数据拟合模型，确定预测变量的统计显着性等度量，然后使用模型进行预测。
这适合哪些缺失的数据框架？是否有任何特殊考虑与更详细的解释变量仅在给定时间点之后才可用这一事实相关，而不是分散在整个历史样本中？
好的，从使用历史数据的经验来看，更多的历史可能会使回归拟合看起来更好，但如果预测是练习的重点，一般的答案会被警告。在数据反映“世界”非常不同的时期的情况下，相关性的稳定性值得怀疑。这尤其发生在市场和法规不断发展的经济学中。
这也适用于房地产市场，此外，房地产市场可能具有较长的周期。例如，抵押贷款支持证券的发明改变了抵押贷款市场，打开了抵押贷款的闸门，不幸的是，投机也随之而来（实际上有一整类无文件/低文件贷款，称为 lier 贷款）。
测试政权变化的方法对于以非主观方式决定何时排除历史特别有价值。
通常，这可以看作是一个有界参数值问题。据我了解您的问题，您的数据早期的信息量较少（未知质量的抵押品 [Cu]），而您的数据中的信息量更多（高 [Ch]、中 [Cm] 或低 [Cl] 质量的抵押品）以后的数据。
如果您认为模型的未观察到的参数不会随时间变化，那么该方法可以很简单，您假设每个参数的点估计为 Cl < Cm < Ch 和 Cl <= Cu <= Ch。逻辑是 Cl 是最差的，Ch 是最好的，所以当数据未知时，它必须介于或等于这些数据之间。如果您愿意稍加限制，并假设在前 15 年并非所有抵押品质量都是高或低的，您可以假设 Cl < Cu < Ch，这使得估计变得更加简单。
在数学上，这些可以用类似的东西来估计：
Cu 中的 logit 函数将值限制在 Cl 和 Ch 之间，而不限制它相对于 Cm。（也可以使用介于 0 和 1 之间的其他函数。）
模型的另一个区别应该是方差应该被结构化，以便残差方差取决于时间段，因为每个时期内的信息是不同的。
