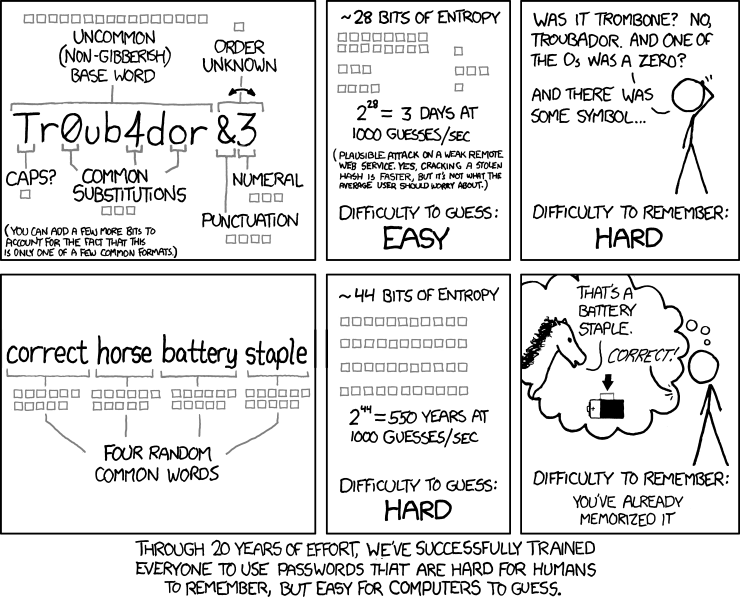
理论视角
让我们在这里算一下。有 26 个字母,10 个数字,比方说大约 10 个特殊字符。首先,我们假设密码是完全随机的(一组中的字符不会比另一组中的字符更可能被使用)。
然后可以将可能的密码数量写成字母的大小和C = s^n字符的数量。密码的熵定义为:sn
log2(C) = log2(s^n) = log2(s)*n
让我们将问题中的数字插入到此:
s n Entropy (bits)
A 52 6 34.2
B 52 10 57.0
C 72 7 43.2
D 26 10 47.0
E 26 5 23.5
所以在这种情况下,C 只是仅次于 B 和 D 的第三好的选择。
实用的观点
但这都是在随机性的假设下。对于人们如何生成密码,这不是一个合理的假设。人类只是不这样做。因此,我们必须选择一些其他假设来了解密码是如何生成的,以及攻击者在她的字典中尝试密码的顺序。
一个不无道理的猜测是,许多字典以单词开头,然后才继续进行替换和添加特殊字符。在这种情况下,短密码中的单个特殊字符将比一个非常长且常见的单词更好。但另一方面,如果攻击者知道总是使用特殊字符,她会先尝试这些密码。另一方面,字典可能以完全不同的原则为中心(例如在泄露的数据库中出现的情况)。
我可以一直猜测这件事。
为什么是问题而不是答案是错误的
问题是密码的生成方式有很多可供选择的原则,我可以任意选择一个来使几乎任何答案都是正确的。因此,整个问题毫无意义,只会掩盖世界上任何密码策略都无法强制执行的重要观点:密码包含的字符不是使其强大 - 而是它是如何生成的。
例如,Password1!包含大写、小写、数字和特殊字符。但这不是很随机。ewdvjjbok另一方面,只包含小写但更好,因为它是随机生成的。
他们应该做的
如果您只是停止依赖非常容易出错和有限的人类记忆,那么字符集和长度就不再是您必须相互权衡的限制因素。你可以拥有丰富的两者。
一种方法是使用密码管理器。正如Dan Lowe在评论中指出的那样,这对医院来说可能不是一个可行的选择。第二种选择是使用某种双因素身份验证(例如硬件令牌或钥匙卡),使第一个因素(密码)的安全性变得不那么重要。
这是系统管理员而不是最终用户的责任来实施。他们必须提供允许最终用户以实用和安全的方式执行其工作的工具。再多的用户教育也无法改变这一点。