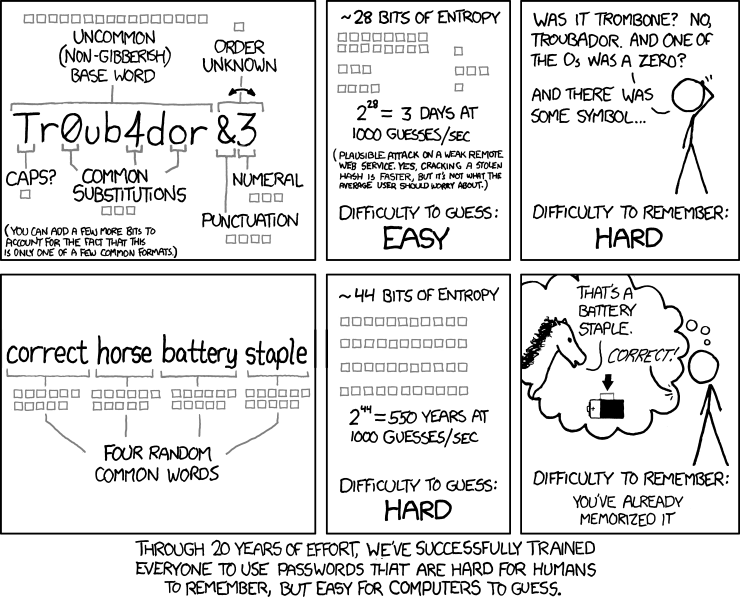
XKCD #936: 短复杂密码,还是长字典密码?
我认为这部漫画最重要的部分,即使它在数学上弄错了(它没有),在视觉上强调选择强密码(或者实际上是密码策略)有两个同样重要的方面,一般来说):
- 难以猜测
- 难以记忆
或者,换句话说:
- 计算机方面
- 人性方面
很多时候,在讨论复杂的密码、强策略、到期等(以及概括地说 -所有安全性)时,我们往往过于关注计算机方面,而忽略了人的方面。
尤其是在密码方面(尤其是对于普通用户来说是两倍),人的方面通常应该是最重要的问题。
例如,IT 实施的严格密码复杂性策略(例如XKCD 中显示的策略)多久会导致用户写下密码并将其粘贴到屏幕上?这是过度关注计算机方面的直接结果,而牺牲了人的方面。
我认为这是来自 XKCD 的圣人的核心信息 - 是的,容易猜到是不好的,但很难记住同样如此。这个原则是正确的
。我们应该更频繁地记住这一点,AKA AviD 的可用性规则:
以牺牲可用性为代价的安全是以牺牲安全为代价的。
这是这部漫画中数学的详尽解释:
漫画中的小方框代表对数尺度的熵,即“比特”。每个盒子意味着一个额外的熵。熵是在蛮力攻击中击中正确密码的平均成本的度量。我们假设攻击者知道确切的密码生成方法,包括该方法中随机选择的概率分布。n位的熵意味着,平均而言,攻击者会在找到正确的密码之前尝试2 n-1 个密码。当随机选择是等概率的时,当有2 n时,您有n位熵可能的密码,这意味着攻击者平均会尝试其中的一半。平均成本的定义更为通用,因为它捕获了在密码生成过程中随机选择的情况(通常发生在人类用户的头脑中)不统一的情况。我们将在下面看到一个示例。
使用“位”的意义在于它们相加。如果您有两个彼此独立生成的密码半部分,一个具有 10 位熵,另一个具有 12 位,则总熵为 22 位。如果我们使用非对数标度,我们将不得不相乘:前半部分的2 10个统一选择和另一半的2 12 个统一选择弥补了2 10 ·2 12 = 2 22 个统一选择。加法更容易用小框以图形方式传达,因此我们使用位。
话虽如此,让我们看看漫画中描述的两种方法。我们将从第二个开始,它更容易分析。
“正确的马”方法
这种方法的密码生成过程是:取一个给定的(公开的)2048 个单词(应该是常用单词,好记)的列表。在这个列表中随机选择四个单词,统一且彼此独立:随机选择一个单词,然后再次随机选择一个单词(可能与第一个单词相同),依此类推,选择第三个,然后是第四个字。将所有四个单词连接在一起,瞧!你有你的密码。
每个随机单词选择值 11 位,因为2 11 = 2048,而且,至关重要的是,每个单词都是均匀选择的(所有 2048 个单词都有相同的 1/2048 被选中的概率)并且独立于其他单词(你不t 选择一个单词,以便它与前面的单词匹配或不匹配,特别是,如果它恰好与前面的单词是相同的选择,你不会拒绝它)。由于人类根本不擅长在头脑中进行随机选择,因此我们必须假设随机单词选择是通过物理设备(骰子、掷硬币、计算机......)完成的。
总熵为 44 位,与漫画中的 44 个框相匹配。
“吟游诗人”方法
对于这个,规则更复杂:
- 在给定的有意义单词的大列表中选择一个随机单词。
- 随机决定是否将第一个字母大写。
- 对于符合“传统替换”条件的字母,应用或不应用替换(每个字母随机决定)。例如,这些传统替换可以是:“o”->“0”、“a”->“4”、“i”->“!”、“e”->“3”、“l”-> “1”(规则给出了一个众所周知的详尽列表)。
- 附加一个标点符号和一个数字。
随机词被漫画评为 16 位,这意味着在 65536 个词的列表中统一选择(或在更长的列表中不统一)。单词比英文的要多,大概有 228000 左右,但有的很长,有的很短,有的太少见,根本记不住。“16 位”似乎是一个合理的计数。
大写或不大写第一个字母名义上是 1 位熵(两种选择)。如果用户在脑海中做出选择,那么这将是用户安全感(“大写显然更安全!”)和用户懒惰(“小写更容易输入”)之间的平衡。再一次,“1 位”是合理的。
“传统替换”更复杂,因为符合条件的字母数量取决于基本词;这里是三个字母,因此是 3 位熵。其他单词可能有其他计数,但似乎合理的是,平均而言,我们会找到大约 3 个符合条件的字母。这取决于假定为给定约定的“传统替换”列表。
对于额外的标点符号和数字,漫画给出 1 位用于选择哪个在前(数字或标点符号),然后是 4 位符号和 3 位数字。数字的计数值得解释:这是因为当被要求选择一个随机数字时,人类根本不是制服; 数字“1”被选中的机会大约是“0”的 5 到 10 倍。在心理因素中,“0”具有不好的含义(虚空、黑暗、死亡),而“1”则具有积极的含义(获胜者、冠军、顶级)。在中国南方,“8”非常流行,因为“八”的发音与“运气”的发音相同;同样,“4”由于与“死亡”一词谐音而被回避。攻击者将首先尝试数字为“1”的密码,从而使他能够从用户选择的不一致性中受益。
如果数字的选择不是由人脑而是由一个不偏不倚的设备做出的,那么我们得到的熵是 3.32 位,而不是 3 位。但这对于说明目的来说已经足够接近了(我很理解 Randall Munroe 不想绘制部分方框)。
标点符号的四位有点低调;ASCII中有 32 个标点符号,都比较容易在普通键盘上输入。这意味着 5 位,而不是 4。同样,如果符号是由人类选择的,那么某些符号会比其他符号更常见,因为人类很少想到“#”或“|” 作为“标点符号”。
总共28 位是正确的,尽管它取决于一些随机选择的精确细节,以及“传统替换”列表(这会影响符合条件的字母的平均数量)。使用计算机生成的密码,我们可能希望大约 30 位。与“正确马”方法的 44 位相比,这仍然很低。
适用性
上面的段落表明漫画中的数学是正确的(至少在这些条件下可以预期的精度——那是网络漫画,而不是研究文章)。它仍然需要以下条件:
攻击者知道“密码生成方法”。这是@Jeff 不相信的部分。但这是有道理的。在大型组织中,安全人员会发布此类密码生成指南。即使他们没有,人们也有谷歌和同事,并且会倾向于使用大约十几个规则中的一个。漫画对此做了规定:“您可以添加更多位来说明这只是少数常见格式之一的事实”。
底线:即使您将方法“保密”,也不会那么秘密,因为您或多或少会自觉地遵循“经典”方法,而这种方法并不多。
随机选择是随机且统一的。这对于人类用户来说很难实现。您必须说服他们使用具有良好随机性的设备(硬币,而不是大脑),并接受结果。这是我原始答案的要点(转载如下)。如果用户改变了选择,如果只是在他们得到的密码“不喜欢他们”的情况下通过生成另一个密码,那么他们就背离了随机均匀性,只能降低熵(最大熵是通过均匀随机性实现的;你不能变得更好,但你可以变得更糟)。
正确的答案当然是 @AviD。漫画中的数学是正确的,但重要的是,好的密码必须既难猜又好记。漫画的主要信息是表明常见的“密码生成规则”在两个方面都失败了:它们使密码难以记住,但密码并不难猜。
它还说明了人类思维在评估安全性方面的失败。“Tr0ub4dor&3”看起来比“correcthorsebatterystaple”更随机;相同的想法只会因为错误的原因而给后者加分,即普遍(但被误导)认为密码长度会产生强度。它不是。密码不强,因为它很长;它很强大,因为它包含很多随机性(我们一直在讨论的所有熵位)。额外的长度只允许通过为随机性提供更多空间来获得更大的力量;特别是,通过允许易于记忆的“温和”随机性,就像电动马一样。另一方面,一个非常短的密码必然是弱密码,因为只有这么多的熵可以容纳 5 个字符。
请注意,“难以猜测”和“容易记住”并没有涵盖所有关于密码生成的内容;还有“easy to use”,通常表示“易于打字”。长密码在智能手机上是一个问题,但带有数字和标点符号以及混合大小写的密码可以说更糟糕。
原答案:
漫画假设选择一个随机的“常用”词会产生大约 11 位的熵——这意味着大约有 2000 个常用词。这是一个合理的计数。当然,诀窍是进行真正的随机选择。例如,以下活动:
- 随机选择四个单词,然后按照最有意义的顺序记住它们;
- 如果这四个单词看起来太难记住,就将它们删除并选择另外四个;
- 用足球运动员的名字替换其中一个词(攻击者永远猜不到!);
...都减少了熵。让您的用户真正使用真正的随机性并接受结果并不容易。
同样的用户可能会抱怨输入长密码的麻烦(如果输入涉及智能手机,我必须说我非常了解他们)。不开心的用户永远不是一件好事,因为他会开始寻找让他的生活更轻松的对策,例如将密码保存在文件中并通过复制和粘贴“输入”密码。用户通常可以通过这种方式获得惊人的创意。因此,在安全方面,长密码往往会适得其反。
两个密码,基于rumkin.com 的密码强度检查器:
Tr0ub4dor&3
- 长度:11
- 强度:合理——这个密码在密码学上是相当安全的,熟练的黑客可能需要一些好的计算能力来破解它。(很大程度上取决于实施!)
- 熵:51.8 位
- 字符集大小:72 个字符
和
正确的马电池订书钉
- 长度:28
- 强度:强- 此密码通常足以安全地保护财务记录等敏感信息。
- 熵:104.2 位
- 字符集大小:27 个字符
确实,在所有其他条件相同的情况下,长度往往会产生非常强的密码——我们在这里看到了这一点。
即使单个字符都限制为,“我们添加了另一个小写字符,所以再次[a-z]乘以 26 ”中暗示的指数往往会主导结果。
换句话说,72 11 < 27 28。
现在,没有明确解决的问题:
这些密码必须手动输入吗?如果是这样,机械地输入密码的每个字符有多困难?在键盘上这很容易,但在智能手机或控制台上......没那么多。
这些密码有多容易记住?
密码攻击有多复杂?换句话说,他们是否真的会尝试 xkcd 所暗示的“用空格分隔的字典单词”、“带标点符号的完整句子”或“leet-speak numb3r 替换”等常见方案?至关重要的是,这就是 XKCD 证明将第一个密码的熵减半的理由!
第 3 点几乎无法回答,我个人认为在实践中极不可能。我预计这将是脑残的蛮力一路获得低调的果实,其余的都忽略了。如果没有任何低调的密码水果(哦,总是有),他们将继续使用下一个潜在的受害者服务。
因此我说这幅漫画在数学上是准确的,但它所暗示的神一般的预测密码攻击在很大程度上是一个神话。这意味着,恕我直言,这两个特定的密码在实践中是一种洗牌,并且会提供类似的保护级别。
我同意长度通常比复杂性更可取。但我认为争议不在于这一点,而在于你想要拥有多少熵。漫画说“合理的攻击”是 1000 次猜测/秒:
“对弱远程 Web 服务的合理攻击。是的,破解被盗的哈希更快,但这不是普通用户应该担心的”
但我看到更多的共识是,网站运营商无法随着时间的推移保护其哈希数据库免受攻击者的攻击,因此我们应该设计密码和哈希算法以抵御窃取哈希以进行离线攻击。如如何安全地散列密码?
这使问题变得更加困难,除了要求用户为每个网站记住自己的密码(例如通过 OpenID 和 OAuth)之外,网站还应该考虑其他选择。这样,用户可以获得一种良好的身份验证方法(甚至可能涉及硬件令牌)并将其用于 Web 访问。
但是好的密码散列也可以通过好的算法、更长的长度和书签工具来完成。在服务器上使用上述问题中描述的技术(即 bcrypt、scrypt 或 PBKDF2),并在Is there a method to generate site-specific passwords that can be executed in my own head? 在用户/客户端使用SuperGenPass(或SuperChromePass )。