L-BFGS 何时优于 GD？

计算科学 收敛 准牛顿
2021-12-16 18:19:57

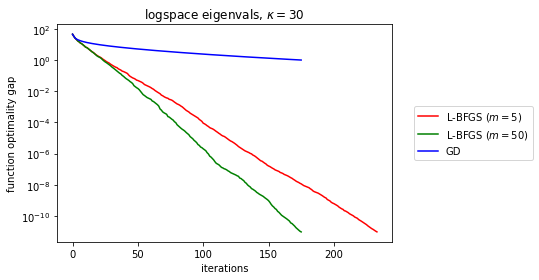
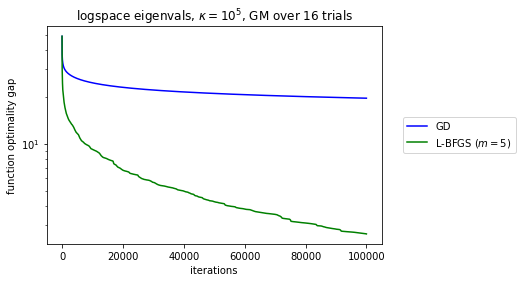
在实践中，L-BFGS 经常与其他不精确的 QN 方法相媲美，它在 Hestenes-Stiefel CG 和 BFGS 之间提供了一种中间立场，因为内存从零变为无穷大（数值优化第 7 章）。许多经验结果表明 L-BFGS 优于 GD，至少在某些大型设置类别中，例如非常强的凸函数和平滑函数。

Liu 和 Nocedal 1989证明了 L-BFGS 下降方向角与梯度在ķ-第一次迭代，θķ, 满足下限因2⁡θķ≥δ>0最终，在中等平滑度下确保类似 GD 的收敛特性：由于下降与 GD 足够一致，在满足 Wolfe 条件的线搜索下，我们得到全局最终收敛，对于平滑和强凸函数，我们实现线性收敛。

然而因2⁡θķ≥δ结果，局部和全局收敛特性来自关于满足 Wolfe 条件的任何下降方法的一般定理。L-BFGS 没有什么特别之处。事实上，用于的不等式因2⁡θķ≥δ结果似乎随着内存的增加而变弱。

具有较差常数的线性局部速率是违反直觉的，感觉就像理论和实践之间的差距。

是否有任何已知的理论结果，其中 L-BFGS 在足够规则的设置中提高了 GD 的线性速率（甚至它的平滑常数），理想情况下，以一种随着内存使用单调提高的方式？

1个回答

（不完全是我的问题的答案，而是一些经验性实验，这些实验可能会指导对二次函数的 L-BFGS 迭代的最坏情况分析应该产生什么结果）。我测试了 GD 和 L-BFGS 的直接翻译算法伪代码实现。在此处查看代码和我的所有实验。即使在你能想到的最好的设置中，一个具有中等条件数的二次函数，L-BFGS 也没有表现出超线性。一般来说，看起来 L-BFGS 的行为基本上就像 GD 的条件更好的版本。

以下是一些快速的要点：

  • 无论内存如何，L-BFGS 收敛顺序看起来都是线性的
  • 不出所料，L-BFGS 在条件良好的二次设置中占主导地位，因为线性速率要好得多。
  • 有趣的是，在我的 vanilla 实现中，高内存 L-BFGS 是不稳定的。
  • 内存的增加似乎线性地提高了有效线性速率。
  • 条件编号显示相同(1-κ-1)类似于 L-BFGS 和 GD 的线性收敛速度的行为。

gd-vs-lbfgs

编辑从评论中回答布赖恩的问题：非常高κ=105, scipy 的不精确 Wolfe 线搜索对于GD 和 L-BFGS都无法终止（米=5）。切换到 Armijo，我得到了嘈杂的下降，所以我用相同的对数空间奇异值重新采样了几个不同的最小二乘问题，并对得到的下降曲线进行几何平均。相同的模式成立（最终是线性的，L-BFGS 占主导地位），但每个人的利率都要低得多。

病态的

其它你可能感兴趣的问题
上一篇搜索引擎算法的最坏情况复杂度 下一篇学生应该复制哪些算法（论文）才能进入计算流固耦合领域？