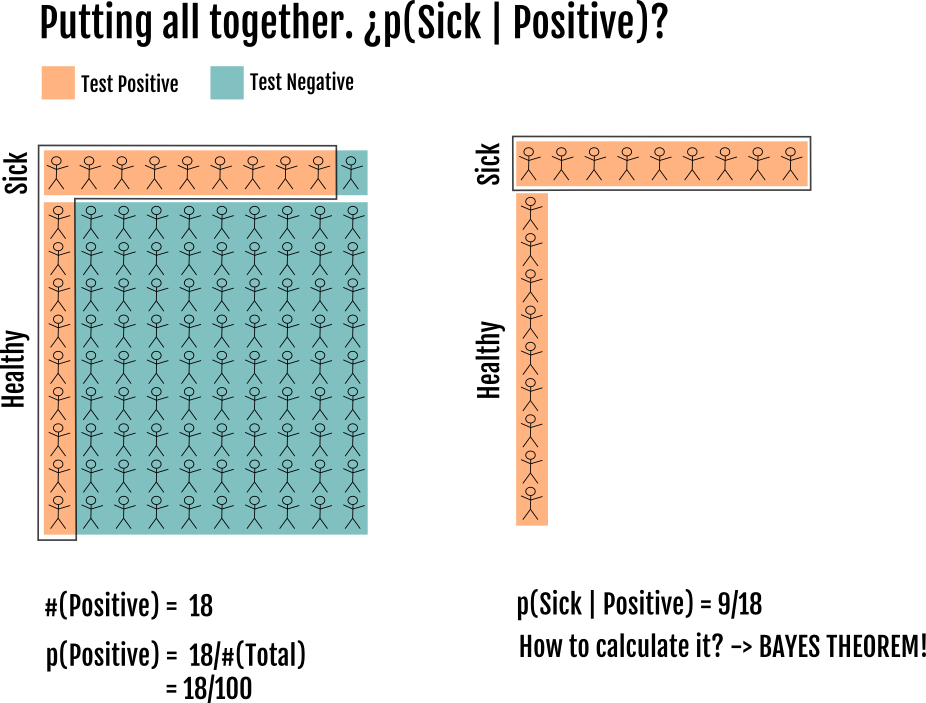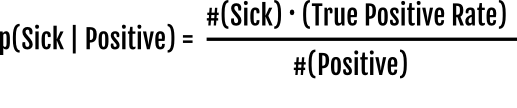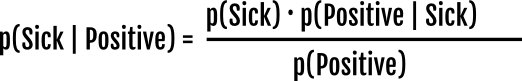基本上只需绘制两个重叠圆圈的维恩图，这些圆圈应该代表一组事件。称它们为 A 和 B。现在两者的交集是 P(A,B)，可以读取 A AND B 的概率。根据概率的基本规则，P(A,B) = P(A | B) P （乙）。而且由于 A 与 B 没有什么特别之处，所以它也一定是 P(B|A) P(A)。将这两者等同起来就可以得到贝叶斯定理。

贝叶斯定理真的很简单。由于两个原因，贝叶斯统计更难。一个是从谈论骰子的随机角色到某些事实为真的概率需要一些抽象。它要求你有一个先验，而这个先验会影响你最终得到的后验概率。而且，当您必须沿途排除很多参数时，就很难确切地看到它是如何受到影响的。

有些人发现这似乎是一种循环。但实际上，没有办法绕过它。使用模型分析的数据不会将您直接引向真相。什么都没有。它只是让您以一致的方式更新您的信念。

贝叶斯统计的另一个难点是除了简单的问题之外，计算变得相当困难，这就是为什么要引入所有数学来处理它的原因。我们需要利用所有可以使计算更容易的对称性，或者求助于蒙特卡罗模拟。

所以贝叶斯统计很难，但贝叶斯定理真的一点也不难。不要想太多！它直接源于“AND”运算符在概率上下文中是对称的这一事实。A AND B 与 B AND A 相同，每个人似乎都直观地理解了这一点。

高尔顿在 1800 年代后期以两级梅花形非常清楚地描绘了解释它的物理论据。

参见 Stigler, Stephen M. 2010 中的图 5。达尔文、高尔顿和统计启示。皇家统计学会杂志：A 系列 173(3):469-482。

我在这里有一个基本的动画（需要足够的 pdf 支持才能运行）。

我还把它变成了一个关于橙子落在高尔顿头上的寓言，我以后会尝试上传。

或者您可能更喜欢这里的 ABC 拒绝图片。

一个基于它的练习在这里。

这篇2020 年 1 月 10 日关于 Medium 的文章仅用一张图片进行了解释！假设

• 一种罕见疾病只感染1/1000 美元的人。
• 测试以 99% 的准确率识别疾病。

如果有 100,000 人，则有 100 人患有罕见病，其余 99,900 人没有。如果这 100 名患者接受检测，$\color{green}{99}$检测结果为阳性，$\color{red}{1}$检测结果为阴性。但我们通常忽略的是，如果对 99,900 名健康人进行测试，其中 1%（即$\color{#e68a00}{999}$）将测试为误报。

现在，如果您检测呈阳性，那么您必须是检测呈阳性的$\color{green}{99}$患病者中的$1$ 。检测呈阳性的总人数为$\color{green}{99}+\color{#e68a00}{999}$。因此，当您检测呈阳性时，您患此病的概率是$\dfrac{\color{green}{99}}{\color{green}{99}+\color{#e68a00}{999}} = 0.0901$。

请参阅为什么疾病检测呈阳性可能并不意味着您生病了。贝叶斯定理和条件概率的可视化。| 通过哈维尔 GB | 中等。

让我们使用以下示例，其中 10 人中有 1 人生病。我们表示[原文如此]可以写成 p(生病 | 总人口) = 生病的概率，因为你研究了整个人口 = 0.1。但是在你研究整个人口的情况下，你只需要写 p(Sick)。

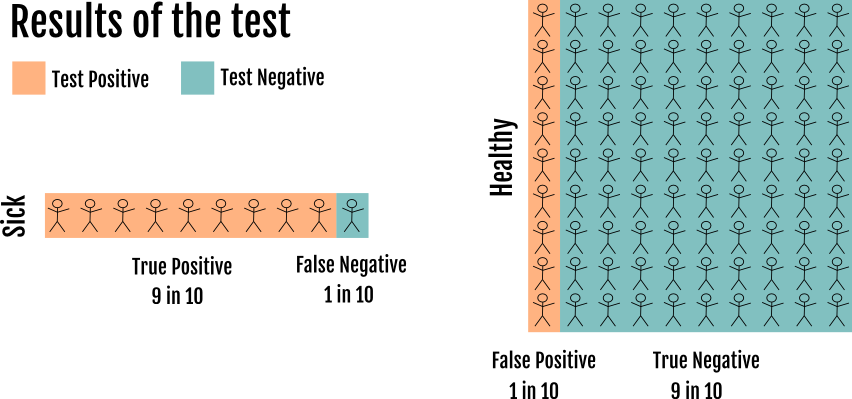
为了简化这个例子，我们假设我们知道哪些是生病的，哪些是健康的，但是在实际测试中你不知道这些信息。现在我们测试每个人的疾病：

患病人群中阳性结果的数量（#(Positive | Sick) 为 9。这些人是真正的阳性，这是众所周知的测试值：

#(阳性 | 生病) = 9
p(阳性 | 生病) = 9/#(生病) = 9/10 = 真阳性率

现在有趣的问题是，如果检测呈阳性，生病的概率是多少？（数学：p（生病|积极））

在上图中，我们掌握了所有信息，因此我们可以将患病的人计入阳性结果中，以表示如果您检测呈阳性，则患病的概率是 9/18 = 50%。但是在现实生活中，您只知道 18/100 的测试结果呈阳性。要知道其中 50% 是误报，您可以使用贝叶斯定理。但我们将在这里推导出它。我们所知道的所有信息是：

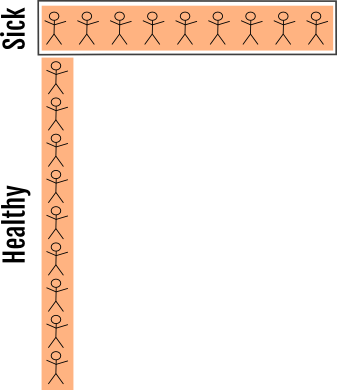
提醒您，我们要计算正方形内的人数#(Sick | Positive)。

直觉是，如果我们知道有 10 个病人 (#(Sick)) 并且真阳性率为 0.9，那么 #(Sick | Positive) = 9。

在数学中：

对于我们在研究人群（阳性结果）中划分的概率，得到：

但是我们不知道到底有多少人生病了，只知道概率，所以我们可以将分数的两个部分除以#(Total)，得到生病的概率和检测呈阳性的概率。

你已经成功地导出了贝叶斯定理！

回顾一下：