通过阻止相应 DAG（有向无环图）中治疗和结果之间的所有后门路径来梳理一个变量/治疗对另一个/结果的因果影响，首先需要绘制一个正确的 DAG。但是我们能确定我们的 DAG 是正确的吗？
您能否指出一个令人信服/严谨/普遍认为是正确的因果研究，该研究通过绘制 DAG 并阻止所有后门路径来估计因果关系？如果您知道这样的研究，为什么您认为 DAG 是正确的？
我一直对使用 DAG 和后门路径进行因果分析很感兴趣，但我没有阅读任何学术期刊，因此我很难评估这种技术是否仅仅是一种有趣的逻辑/理论设置，或者实际上是否实用/有用。
不，我们永远无法确定 DAG 是否正确。这是 DAG 提供的因果推理的基本原则之一。DAG 是对现实的非参数抽象。您会在许多 DAG 文献中找到如下内容：
在因果图中，箭头表示父母对孩子的“直接影响”，尽管这种影响仅相对于某个抽象级别是直接的，因为该图省略了可能调解箭头所表示的影响的任何变量。
这是完全无法避免的。进行药理研究。有很多很多进入市场的药物案例，研究人员不知道导致其产品起作用的实际生物学机制。他们可能有理论，这些理论可以用 DAG 封装。结果分析取决于 DAG 是否正确（在抽象级别上）。其他研究人员可能有不同的理论，因此有不同的 DAG，这是完全可以的。
我们可以首先更一般地思考因果图到底是什么。然后让我们讨论如何实际使用它们作为信息先验，并与观察数据一起，自信地预测因果关系。
因果图是分布内变量（即节点）之间函数关系的有向无环图（DAG）表示。并且图的结构用于编码变量之间的条件依赖或独立。该图本质上以易于理解的视觉格式断言了我们对世界的假设。提供联合分布 p(a,b,c)，相同的分布可以写成：
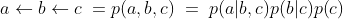
那么哪个因果图是联合分布的正确因果图呢？该示例表明因果图与我们的观察数据的映射是多对一的。多个正确的假设是合理的，并且通常不可能仅通过观察观察数据在它们之间做出明确的选择。
那么我们如何使用观测数据来推断正确的图表呢？对于上述因果图，我们通过调节变量来模拟干预的效果（即，我们强制它采用特定值）。该动作由 p(Y|do(X)) 中的 do-operator 封装，更正式地由 do-calculas 封装，do-calculas 是一种用于因果推理的工具，它允许我们从观测数据中消除需要估计的内容。前门和后门方法只是两扇门，我们可以通过它们消除攀登干预山的所有工作。
可以说，通过删除感兴趣节点的所有传入边，干预将原始联合分布修改为干预后分布。如果我们可以删除所有操作符，则因果查询变得可识别，因此我们可以使用观察数据来估计因果效应。否则，因果查询被认为是不可识别的，并且需要进行真实世界的干预实验来确定因果关系。
虽然研究人员可能永远不会完全相信他们构建的因果图的合理性和完整性，但他们确实有适当的机制来凭经验测试变量集之间的部分关系集合。如果观测数据中不存在相关性和独立性，这可能是图表不准确的信号。然后，研究人员可以迭代地测试和更新因果图，使其更符合观测数据中包含的信息（以及适用的领域知识）。