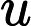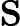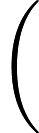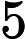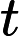我正在尝试使用具有以下边界条件的中心近似的 FD隐式求解 2D 波动方程

$$\begin{align} &u=2\sin\left(\frac{2\pi}{5}t\right)\quad \text{at }x=0\\ &\frac{\partial u}{\partial y}=0 \quad \text{at }y=0\\ &\frac{\partial u}{\partial y}=0 \quad \text{at }y=2\\ &\frac{\partial u}{\partial t}=-\frac{\partial u}{\partial x} \quad \text{at }x=5 \end{align}$$

图形表示为

x=0 处的边界条件生成波。x=5 处的边界条件是指Mur 边界条件，即波不反弹，而只是继续在域外移动。一般方程为

Mur 边界条件在数学上可以表示为

对边界条件进行了分析评估，这些是整个域之后的 7 个方程：

问题- 我已经设法编写了一些代码，包括设置[A]矩阵（方程的 LHS），但是我在制定[b]矩阵（RHS）并通过时间步求解它时遇到了问题。如果有人告诉我如何为第一个等式编写它，我将不胜感激 - 然后我将能够完成剩下的 6 个。

% length, time, height
L = 5; % [m]
h = 2; % [m]

d = 0.25; % space spacing
dt = 0.05; % time increment
M = 100; 
T_max = M*dt; % [s]

nx = floor(L/d); % number of <x> samples
ny = floor(h/d); % number of <y> samples
k = floor(T_max/dt) + 1; % number of time samples

% Constants
alpha = dt/d;
r = dt^2/d^2;

% Number of grid points:
N=nx*ny;

% Initialise matrices
U = zeros(N,1);
b = zeros(N,1);
x = zeros(N,1);
A = zeros(N,N);

% Set numbering for the [A] matrix
num = 1;
for i=1:nx
    for j=1:ny
        number(i,j) = num;
        num = num + 1;
    end 
end 

% [A] matrix - boundary conditions
    % Case 1 
    for i=2:nx-1
        for j=2:ny-1
            ii=number(i,j);
            A(ii, number(i, j)) = 1+4*r;
            A(ii, number(i+1, j)) = -r;
            A(ii, number(i-1,j)) = -r;
            A(ii, number(i, j+1)) = -r;
            A(ii, number(i, j-1)) = -r;
        end 
    end       

    % Case 2
    for i=1
        for j=2:ny-1
            ii=number(i,j);
            A(ii, number(1, j)) = 1+4*r;
            A(ii, number(2, j)) = -r;
            A(ii, number(1, j+1)) = -r;
            A(ii, number(1, j-1)) = -r;
        end 
    end 

    % Case 3 
    for i=nx
        for j=1:ny
            ii=number(i,j);
            A(ii, number(nx, j)) = 1+alpha;
            A(ii, number(nx-1,j)) = 1-alpha;
        end 
    end 

    % Case 4 
    for i=2:nx-1
        for j=1
            ii=number(i,j);
            A(ii, number(i, j)) = 1+4*r;
            A(ii, number(i-1,j)) = -r;
            A(ii, number(i+1,j)) = -r;
            A(ii, number(i, j+1)) = -2*r;
        end 
    end 

    % Case 5
    for i=1
        for j=1
            ii=number(i,j);
            A(ii, number(i,j)) = 1+4*r;
            A(ii, number(i+1,j)) = -r;
            A(ii, number(i, j+1)) = -2*r;
        end 
    end 

    % Case 6
    for i=2:nx-1
        for j=ny
            ii=number(i,j);
            A(ii, number(i,j)) = 1+4*r;
            A(ii, number(i-1,j)) = -r;
            A(ii, number(i+1, j)) = -r;
            A(ii, number(i, j-1)) = -2*r;
        end 
    end 

    % Case 7
    for i=1
        for j=ny
            ii=number(i,j);
            A(ii, number(i,j)) = 1+4*r;
            A(ii, number(i+1, j)) = -r;
            A(ii, number(i, j-1)) = -2*r;
        end
    end

% Inverse of [A] matrix
A_inv = inv(A);

% [b] matrix (RHS)
time = 0;
for t=1:M
    % Computing [b] matrix
    for i=1:nx
        for j=1:ny
            ii = number(i,j);
            % U(1,1) = 2*sin((2*pi/5)*(t*dt));

            % Case 1
            for i=2:nx-1
                for j=2:ny-1

                end 
            end 
            % or

            for i=1:nx
                for j=1:ny

                end 
            end 

        end 
    end 

    % The solution vector
    x = A_inv*b;

    % 2D matrix from the solution vector