我从图书馆的文档中遵循这个例子scikit-fuzzy，但无法弄清楚模糊规则背后的数学。
这是该示例的简短版本。
食品质量为 6.5（中等）
服务为 9.8（很好）
食品质量和服务范围为 [0, 10]
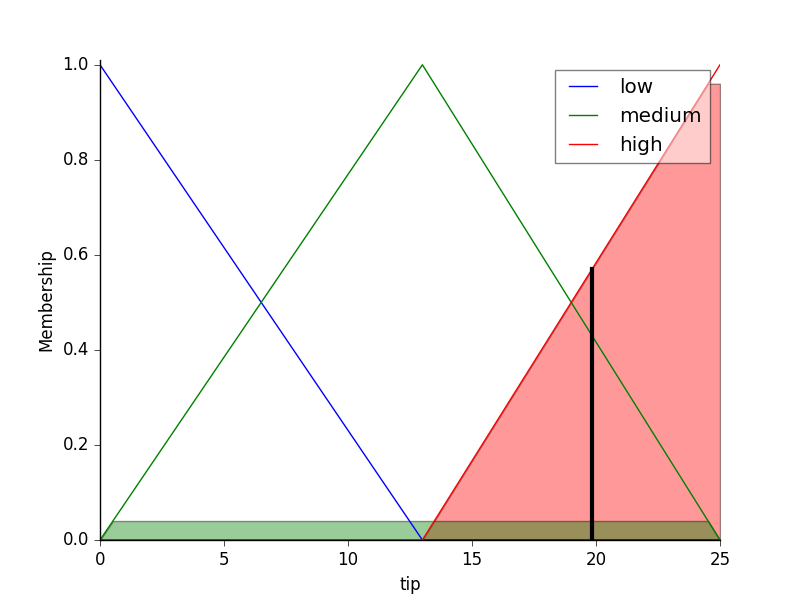
小费金额范围为 [0, 25]规则：
- 如果食物不好或服务很差，那么小费会很低
- 如果服务可以接受，那么小费将是中等的
- 如果食物很棒或服务很棒，那么小费会很高。
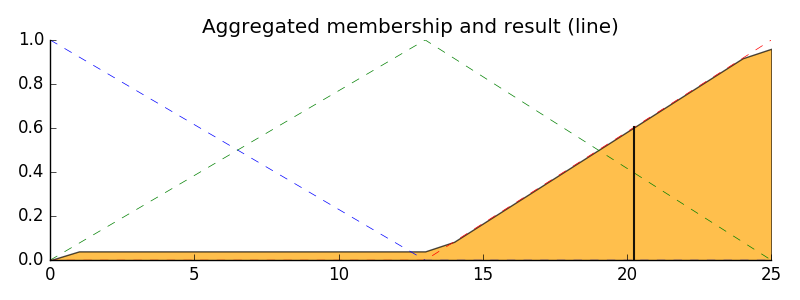
计算的小费金额为20.2。我的问题是，这是如何计算的？
我以这种方式手动解决了这个问题：
由于食物“很棒”，我应用了规则 3.
质量为 % = 6.5/11（11 是评分范围）
服务为 % = 9.8/11
max(6.5/11 , 9.8/11) * 26 = 23.16 (26为小费范围)
他们使用的方法是这样的。
由于质量和服务不属于“差”/“差”类别，因此不属于“低小费”类别。“可接受”类别中的服务会员资格为 0.04，这意味着“中等小费”类别中的会员资格为 0.04。最后，质量在“伟大”类别中的成员约为 0.3，但服务在“惊人”类别中的成员为 0.96。在他们的模糊逻辑方案中，他们使用 Max 代替 OR，因此这转化为“大尖端”类别中的 0.96 成员。
这是链接文档的最后一个图中显示的内容。
他们在 Abdullah 在评论中分享的链接中提到，这不是“去模糊化”结果的唯一方法，但这是他们在这里所做的。我不知道这是如何在代码中实现的，但在这种情况下可以（大致）使用以下公式确定。
算出这个结果，最终去模糊的小费量约为 19.8。
这使我们非常接近步骤 2 中的数字更准确的估计，但它并不完全相同，因为我没有考虑分布两侧的小排除区域。但是，这仍然应该让您了解他们用于计算此值的过程。