贝叶斯定理是概率论的一个相对简单但基本的结果，它允许计算某些条件概率。条件概率只是那些反映一个事件对另一事件概率的影响的概率。

简单地说，它最著名的形式是，假设给定新数据的概率（P(H|D)；称为后验概率）等于以下等式：给定假设的观察数据的概率 ( P(D|H)；称为条件概率），乘以新证据之前理论为真的概率（P(H)；称为 H 的先验概率），除以看到该数据的概率，周期 ( P(D )；称为 D) 的边际概率。

形式上，等式如下所示：

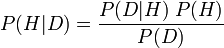
贝叶斯定理的重要性很大程度上是因为它的正确使用是概率学派之间争论的焦点。对于主观贝叶斯主义者（将概率解释为主观信念程度），贝叶斯定理通过将主观概率判断插入方程并运行它，为理论测试、理论选择和其他实践提供了基石。对于频率论者（将概率解释为限制相对频率），这种对贝叶斯定理的使用是一种滥用，他们努力改为使用有意义的（非主观的）先验（就像在另一种概率解释下的客观贝叶斯一样）。

抱歉，这里似乎有些混乱：贝叶斯定理不适合讨论永无止境的贝叶斯频率论辩论。这是一个与两种思想流派一致的定理（假设它与 Kolmogorov 的概率公理一致）。

当然，贝叶斯定理是贝叶斯统计的核心，但该定理本身具有普适性。频率论者和贝叶斯论者之间的冲突主要与如何定义先验分布有关。

所以，如果问题是关于贝叶斯定理（而不是贝叶斯统计）：

贝叶斯定理定义了如何计算特定的条件概率。例如，假设您知道：某人患有症状 A 的概率，假设他们患有疾病 X p(A|X)；一般人患疾病 X p(X) 的概率；一般某人出现症状 A p(A) 的概率。有了这 3 条信息，您可以计算某人患有疾病 X 的概率，假设他们有症状 A p(X|A)。

贝叶斯定理是一种旋转条件概率的方法$P(A|B)$到另一个条件概率$P(B|A)$.

对某些人来说，一个绊脚石是$P(B|A)$. 这是一种通过仅考虑那些事件来减少可能事件空间的方法$A$肯定会发生（或者是真的）。例如，掷出的公平骰子出现六的概率，$P(\mbox{dice lands six})$, 是 1/6，但是骰子落在 6 的概率是因为它落在了偶数上，$P(\mbox{dice lands six}|\mbox{dice lands even})$, 是 1/3。

您可以自己推导出贝叶斯定理，如下所示。从条件概率的比率定义开始：

$P(B|A) = \frac{P(AB)}{P(A)}$

在哪里$P(AB)$是联合概率$A$和$B$和$P(A)$是边际概率$A$.

目前该公式没有参考$P(A|B)$，所以让我们也写下它的定义：

$P(A|B) = \frac{P(BA)}{P(B)}$

完成这项工作的小技巧是看到$P(AB) = P(BA)$（由于布尔代数在所有这些之下，您可以通过显示$AB = BA$)，所以我们可以写：

$P(A|B) = \frac{P(AB)}{P(B)}$

现在将其插入公式中$P(B|A)$, 只需将上面的公式改写为$P(AB)$在左边：

$P(AB) = P(A|B)P(B)$

嘿presto：

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

至于以这种方式旋转条件概率的意义何在，考虑一个常见的例子，即在某人有症状的情况下尝试推断某人患有疾病的概率，即我们知道他们有症状——我们可以看到它 - 但我们无法确定他们是否患有疾病并且必须推断它。我将从公式开始并返回。

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

所以要解决这个问题，您需要知道症状的先验概率、疾病的先验概率（即，症状和疾病的常见或罕见程度）以及在我们知道某人有症状的情况下某人有症状的概率一种疾病（例如，通过昂贵、耗时的实验室测试）。

它可能比这复杂得多，例如，如果你有多种疾病和症状，但想法是一样的。更一般地说，如果你有一个关于原因（例如，疾病）和结果（例如，症状）之间关系的概率论，并且你需要向后推理（例如，你看到一些你想要的症状，那么贝叶斯定理通常会出现）推断潜在疾病）。

统计学有两个主要流派：常客和贝叶斯。

贝叶斯定理与后者有关，可以看作是一种理解理论为真的概率如何受到新证据影响的方式。这被称为条件概率。你可能想看看这个来掌握数学。