基本上RK 所做的可以看作是某种插值。正如您在图 1 中看到的，与 Euler 相比，RK 的优势在于其更大的稳定区域，因此我认为您应该运行一系列测试来检查您是否确实在稳定区域内。如果您选择自己先进行插值，那么您将引入不应该存在的其他相关性......我认为如果可以的话，最好减少计算向量场的时间步长。

最好不要使用插值，因为我假设您默认使用三次样条线，即而 RK4 是。您必须进行错误分析，看看这是否会降低您的准确性，我认为它很可能会降低。也就是说，如果你做一个非常高阶的插值，那么你很好。要知道你需要做多高的订单，你真的必须查看方程式，输入误差项，检查展开式，看看它在哪里结束。$\mathcal{O}(h^3)$$\mathcal{O}(h^4)$

我做了一堆测试，似乎我的问题的答案是使用 Runge-Kutta 插值确实有效果。但是，在积分器中使用比输入数据更短的时间步似乎不会产生很大的影响（不过，我仍然需要插值，因为龙格-库塔方法会在中间时间点评估导数）。

我仅针对输入数据中空间和时间分辨率之间的比率这样的情况进行了测试，即我通常只会在一个时间步长内移动空间网格间距的一小部分（1/10 - 1/5）。

有趣的是，插值方案的选择似乎在某些情况下会产生影响。

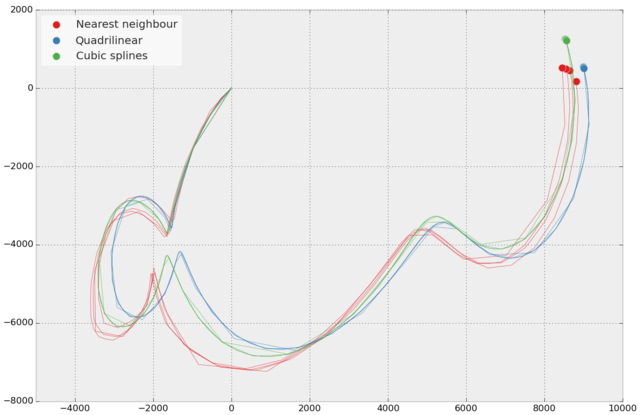
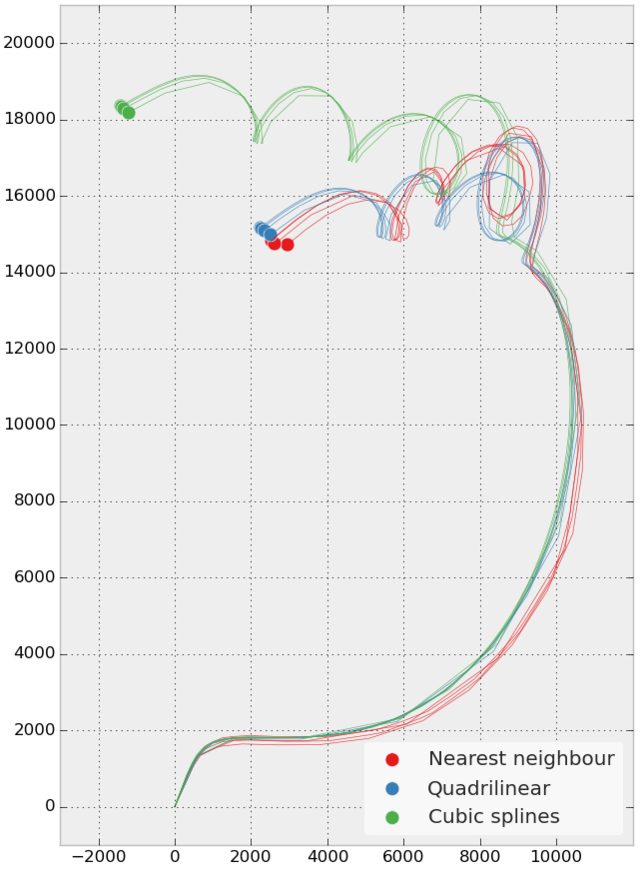
在图中，我使用 4 阶 Runge-Kutta 传输粒子 2 天（顶部）和 3 天（底部），并使用图例给出的插值方案。x 和 y 坐标以米为单位。对于每个方案，我使用了不同的时间步长：2 小时、1 小时、0.5 小时和 0.25 小时。输入数据中的时间步长为 1 小时。本质上，将时间步降低到低于输入数据的时间步对结果的影响很小。但是，从线性插值到三次样条曲线在下面显示的两种情况之一中具有很大的影响。使用样条插值运行程序大约需要三倍的时间。

我想确定哪种方法“最正确”的唯一方法是从同一来源获取更高分辨率的数据，然后比较从高分辨率和低分辨率数据得出的轨迹。